Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bậc ba
Cho hàm số bậc ba \(y=f(x)=ax^3+bx^2+cx+d\).
Ta có \(y'=f'(x)=3ax^2+2bx+c\).
Ta có \(\Delta'_{y'}=b^2-3ac\). Nếu \(b^2-3ac>0\) thì đồ thị hàm số có hai điểm cực trị. Ta cần viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị.
Có nhiều trường hợp, giải phương trình \(f'(x)=0\) ra nghiệm xấu. Toạ độ hai điểm cực trị có số xấu. Làm thế nào để viết phương trình đường thẳng qua hai điểm cực trị.
Giả sử phương trình \(f'(x)=0\) có hai nghiệm phân biệt \(x_1, x_2\). Khi đó toạ độ hai điểm cực trị của đồ thị là \(M(x_1; f(x_1))\), \(N(x_2; f(x_2))\).
Thực hiện phép chia \(f(x)\) cho \(f'(x)\) và giả sử ta được thương \(q(x)\) và dư là \(r(x)=kx+m\). Như vậy \(f(x)=q(x).f'(x)+r(x)\).
Xét đường thẳng \(d: y=kx + m\).
Ta có \(f(x_1)=q(x_1).f'(x_1)+r(x_1)=r(x_1)\), bởi vì \(f'(x_1)=0\), do \(x_1\) là điểm cực trị của hàm số.
Tương tự \(f(x_2)=q(x_2).f'(x_2)+r(x_2)=r(x_2)\), bởi vì \(f'(x_1)=0\), do \(x_1\) là điểm cực trị của hàm số.
Như vậy toạ độ hai điểm \(M, N\) thoả mãn phương trình \(y=kx+m\). Do đó đường thẳng \(d: y=kx+m\) là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bậc ba.
Ví dụ. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y=f(x)=x^3-2x^2-x+1\).
Giải. Ta có \(f'(x)=3x^2-4x-1\). Thực hiện phép chia đa thức \(f(x)\) cho \(f'(x)\) ta được thương là \(\dfrac{1}{3}x-\dfrac{2}{9}\) và dư là \(-\dfrac{14}{9}x-\dfrac{7}{9}\).
Từ đó phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số là \(y=-\dfrac{14}{9}x-\dfrac{7}{9}\).
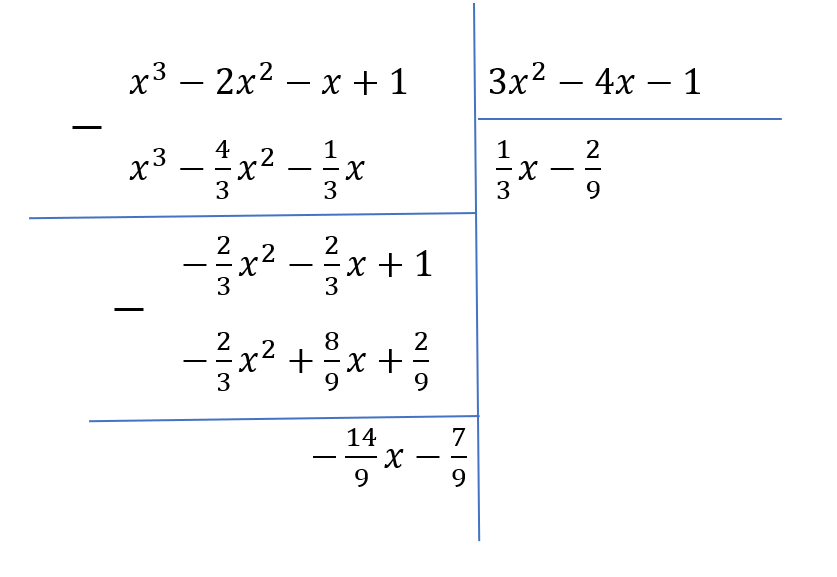

 Định nghĩa góc giữa hai đường thẳng
Định nghĩa góc giữa hai đường thẳng  Góc giữa hai vectơ
Góc giữa hai vectơ  Định lý cosin
Định lý cosin 